この記事では『移動平均』について「だいたい分かった！」を目指します。
移動平均とは、ずばり「ならすための平均」です。
時間とともに変化しやすい値などでよく使われ、その一つのデータだけに注目するよりも、前後の期間の変化を取り込み、ならした方が利用しやすい場合に使われます。
どういうこと？具体例で説明
corサルくん
博士、「ならすための平均」ってどういうこと？
たとえば、ぶたさんがカフェを経営していて、その売上を考えてみよう。
cor博士
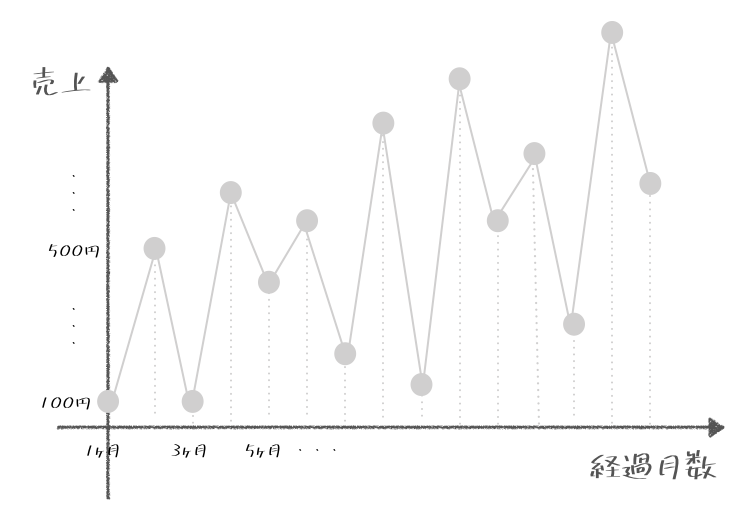
ぶたさんは毎月自分のお店の売上を計算したいんじゃが、月ごとにグラフにするとこんなふうにガタガタになってしまったんじゃ。
cor博士
売上などは、一月単位でみると大きく変わりやすいじゃろ？だから多くの会社でQ（3ヶ月ごと）で売上目標を立てたりするんじゃ。
cor博士
corサルくん
たしかにそうだね！1ヶ月だけの数値で喜んだり悲しんだりするのはなんだかおかしい気もするね。
それに、たとえば3ヶ月に一度季節ごとのイベントがあるとすると、それによって大きく売上が上がったり下がったりしてしまうじゃろ？そういった定期的に売上に大きな変化を与えることがある場合などに、その影響を他の月でならしてしまおうというものが移動平均なんじゃ。
cor博士
つまり、一つだけのデータに注目しては本質を見失ってしまうような、時間によって変化するデータに対してよく使われるものと覚えておくとよいぞ。
cor博士
具体的な方法
corサルくん
具体的にはなにをすればいいの？博士。
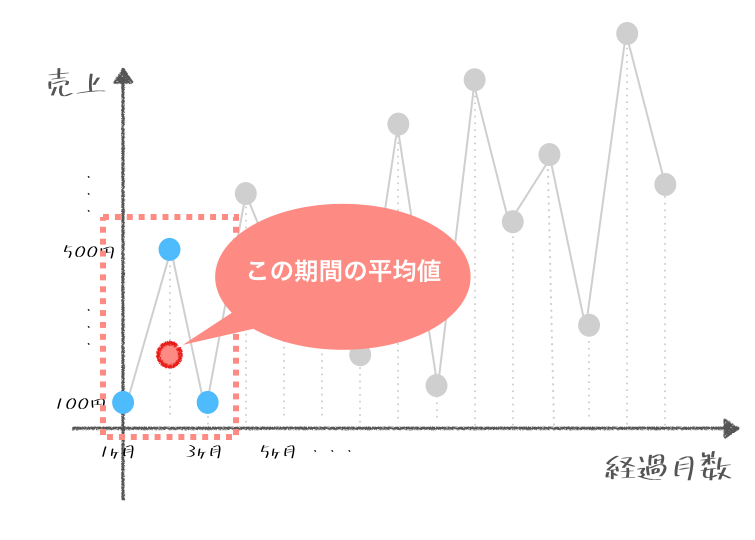
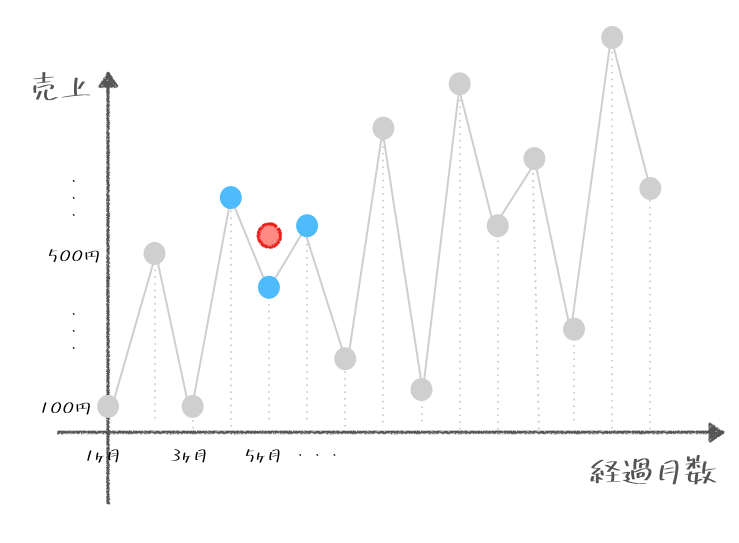
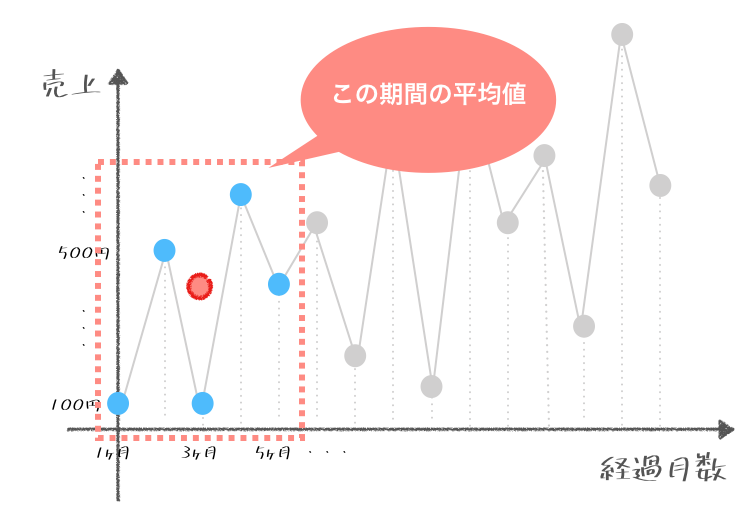
移動平均では基本的に前後のデータを含めた平均をそれぞれ求めていくのじゃ。たとえばこの図のように1ヶ月目だけの売上だけに注目せずに、1ヶ月目、2ヶ月目、3ヶ月目の3ヶ月の期間の平均をまず求めるのじゃ。
cor博士
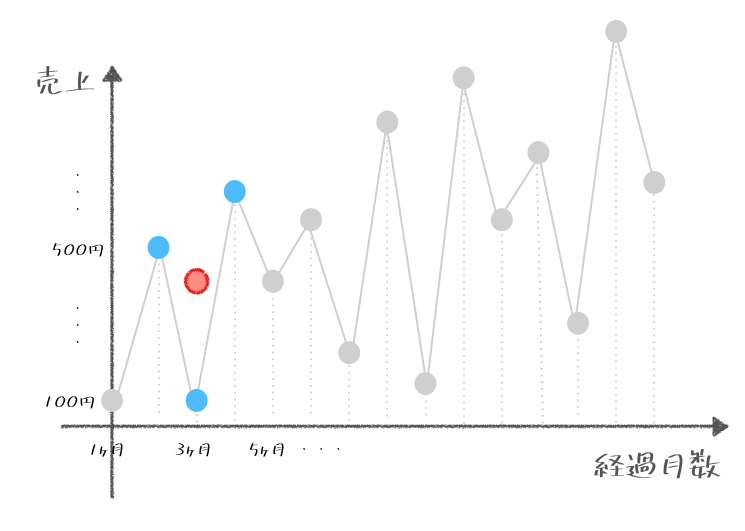
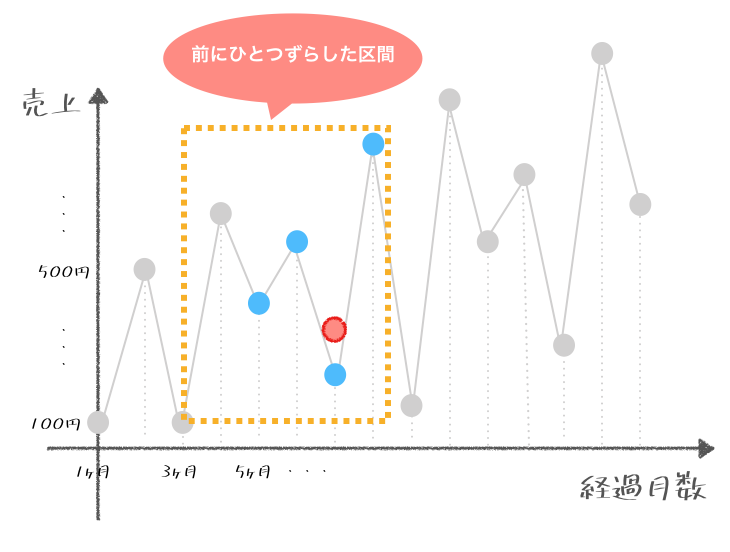
そして、3ヶ月の期間という期間は変えずに、1ヶ月ずつ右にずらしていく。つぎは2ヶ月目、3ヶ月目、4ヶ月目の3ヶ月の期間の平均を求めるのじゃ。
cor博士
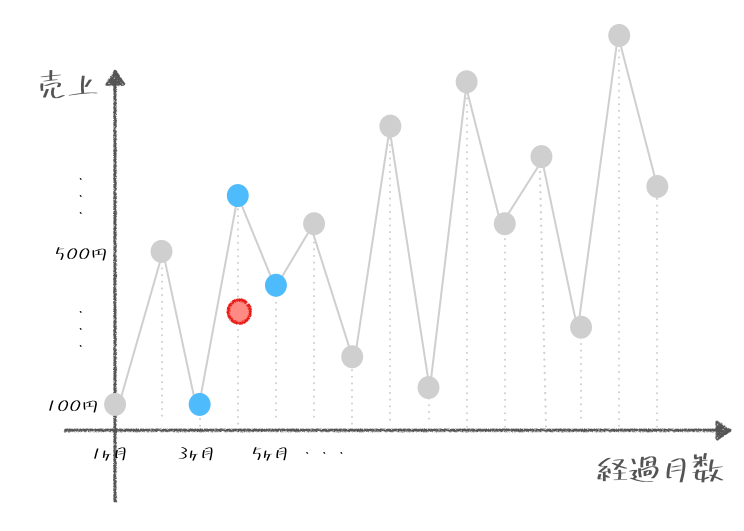
そしてこれを繰り返していき、ぞれぞれ平均値を真ん中の順番のところに書いていくとどうなるかの？
cor博士
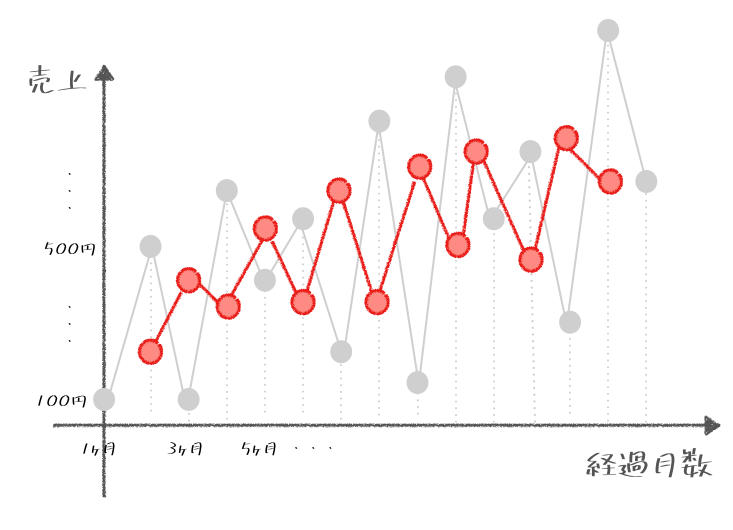
新しくつくった3ヶ月毎の平均を繋げていくと、このように少しなめらかになったグラフができるはずじゃ。
cor博士
これが何を表しているかと言うと、真ん中の月の売上と前後の1ヶ月の売上を足して3で割った値じゃから、「3ヶ月でならされた売上」がそれぞれ出ているはずじゃ。
cor博士
corサルくん
なるほど。前後の値を1つずつ足しているから、その分最初と最後は足せなくてグラフが短くなるんだね！
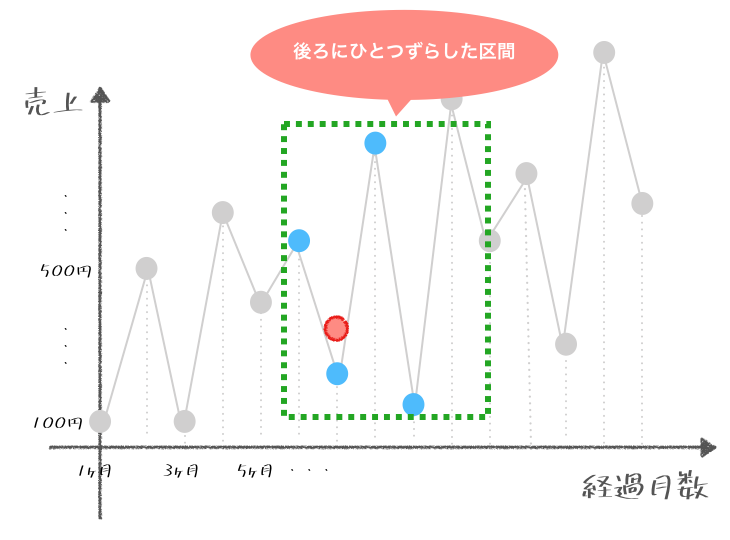
そのとおりじゃ。これを「3ヶ月移動平均」とも呼んだりするぞ。それにな、これはなにも3ヶ月でないといけないという決まりはないのじゃ。こんな風に5ヶ月間の期間で区切ってもよいのじゃよ。
cor博士
cor博士
そのとおりじゃ。これはなにも3ヶ月でないといけないという決まりはないのじゃ。だからこんな風に5ヶ月間の期間で区切ってもよいのじゃよ。これを前回と同じように「５ヶ月移動平均」とも呼んだりするぞ。
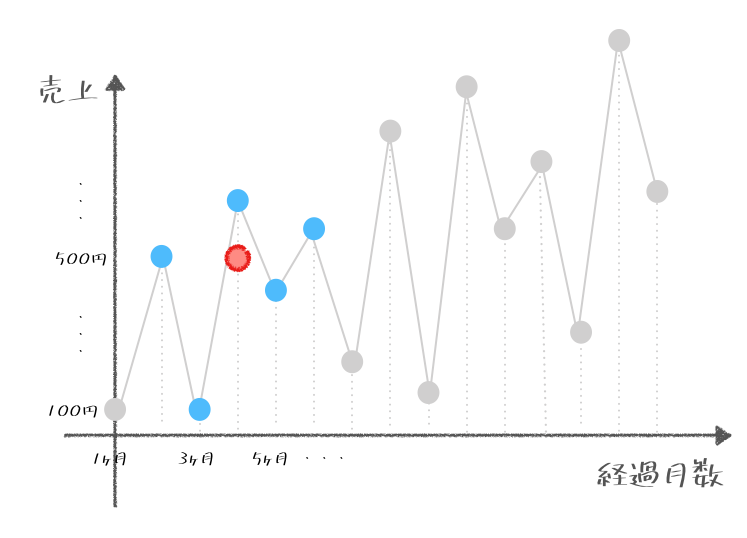
これを同じ様に繰り返してみよう。
cor博士
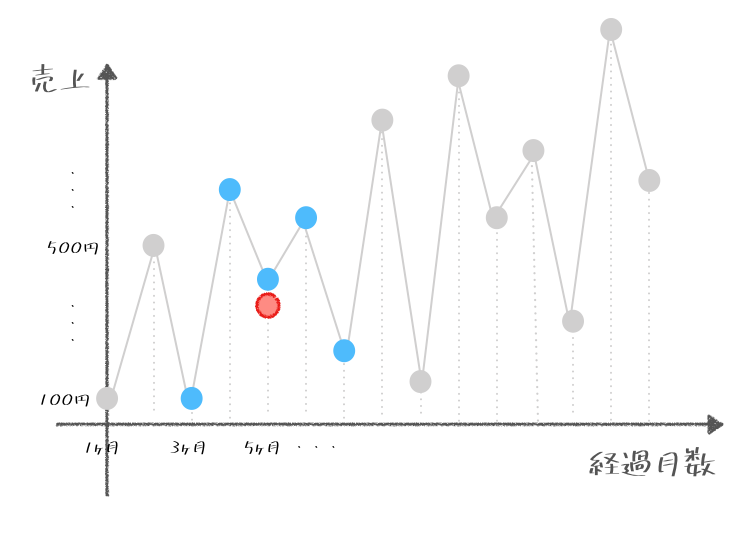
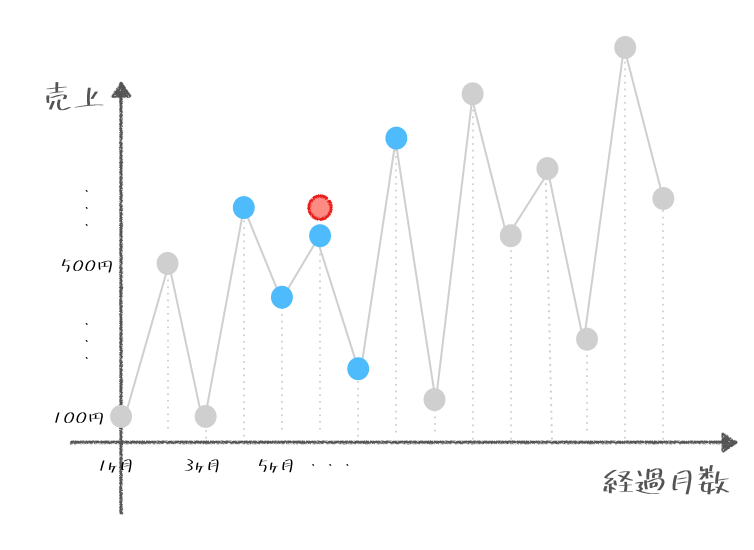
ここでポイントじゃが、期間が長くなったからといって、平均を求める間隔は変わらず、ひとつひとつに対して求めていくんじゃぞ。
cor博士
corサルくん
なるほど。4半期ごと、半年ごとに平均を求めるということとはまた違うんだね！
そうじゃ。そして同じ様に計算した平均を繋げてみると、さらになめらかになったグラフができるんじゃ。
cor博士
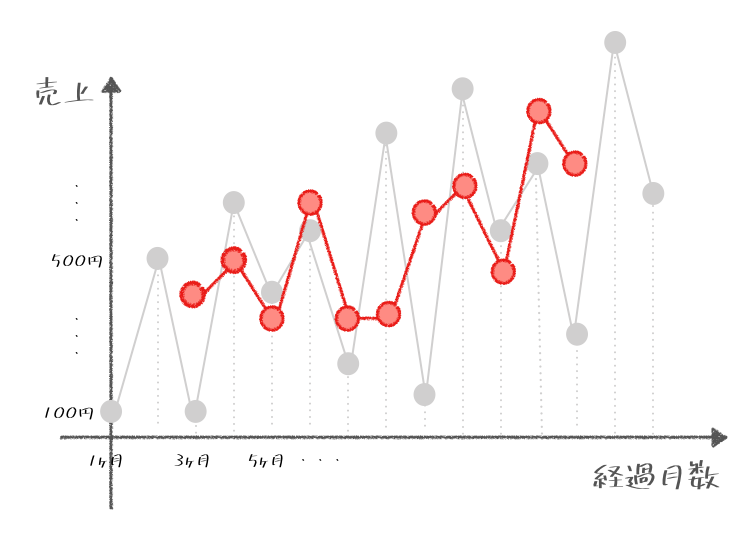
corサルくん
でも今度は最初と最後の2ヶ月間が計算できなかったから、だんだん短くなっているね。
そうなんじゃん。だから移動平均を使うときは、「どのくらいの期間でならされるか」を考えることも重要じゃぞ。この期間を長くしていけば、最終的には全期間の平均を求めることになる。そうすると、そもそも普段よく使う「平均」の値になるのじゃ。
cor博士
corサルくん
おもしろいね！細かい範囲で平均を考えているんだね。
ワンポイント上級者
この記事の例では区間が３ヶ月間、５ヶ月間と奇数の区間で考えましたが、この区間が偶数の場合は計算方法が異なります。
たとえば4ヶ月間の移動平均を求めたい場合はこのように、前2ヶ月と後ろ1ヶ月を加えた4ヶ月間の平均と、前1ヶ月と後ろ2ヶ月を加えた4ヶ月間の平均とを足し更に平均をとり（2で割る）ます。
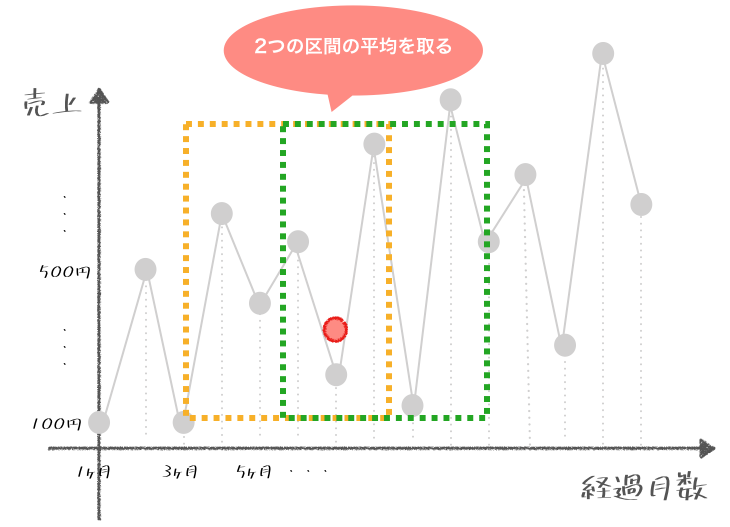
関連用語
- 時系列解析
- トレンド
- 算術平均（一般的な平均）
- 加重平均
- 幾何平均
コメントを残す