この記事では『標準偏差』『分散』について「だいたい分かった!」を目指します。
ずばり標準偏差とは?分散とは?
分散も標準偏差も『ばらつきを測る為の指標』です。標準偏差は分散をより理解しやすい形にしたものです。
『ばらつき』が何を意味しているのか理解できれば、分散も標準偏差も手順にそって計算するだけですので、ここでは『ばらつき』の概念に着目して説明します。こちらのスライドを見てみてください。
なぜ「ばらつき」(分散・標準偏差)の考え方が必要なのか
ばらつきについてはなんとなくイメージを掴んでもらえたと思います。では、なぜこの「ばらつき」の考え方が必要になるのでしょうか。これもスライドで見ていきましょう。
「ばらつき」は平均だけでは表せないグループのことを教えてくれる指標なのです。そのグループが一体どんなデータの集まりなのかを把握する為に様々な代表値が使われますが、その一つの指標なのです。
分散と標準偏差の関係
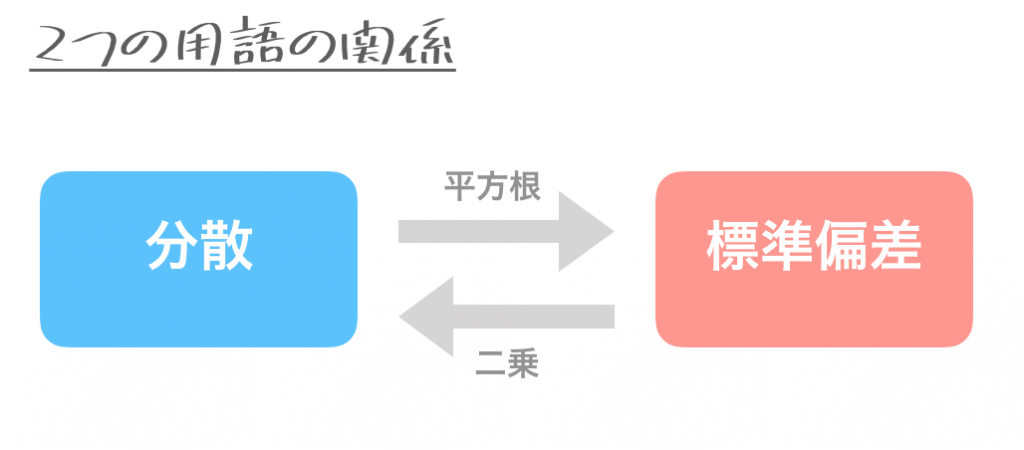
それでは分散と標準偏差の関係はなんでしょうか?とっても簡単です。単に二乗したり、戻したりしたもの。
分散と標準偏差の2つの用語を覚えたらその関係性に注目しよう。標準偏差を二乗したものが分散、分散の平方根(√)をとったものが標準偏差なのじゃ。その後に分散や標準偏差がなんなのかを理解すると覚えやすいぞ。
 cor博士
cor博士
 corサルくん
corサルくん
なんで二乗したり平方根(√)を取ったりややこしいことをするの?
ふむ。それは計算の過程上都合が良いからなんじゃ。
 cor博士
cor博士
平均と分散・標準偏差の関係
分散と標準偏差が「ばらつき」を表す指標、そして分散と標準偏差はちょっとした計算方法の違いで入れ替え可能なほとんど同じようなもの、ということがなんとなくイメージできたかと思います。
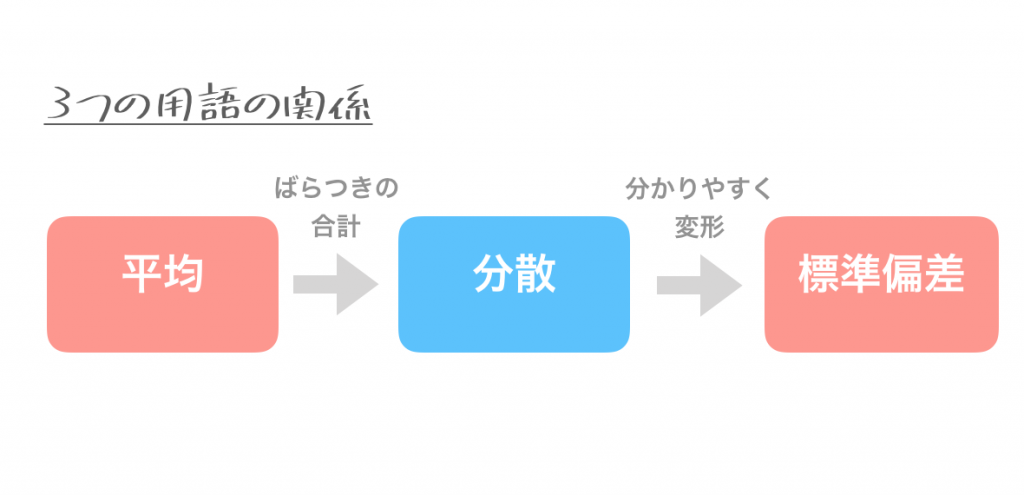
それではこの「ばらつき」はどの様に求めるのでしょうか?これも簡単。単純に平均からどれだけ離れているか(差)を合計したものなのです。
計算方法は差を二乗して足していく・・・と少しややこしいので、用語だけ理解したい人は覚えなくて構いません。この関係性だけ覚えていてください。
関連用語
- 仮説検定
- p値

コメントを残す